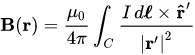Motor Questions

This project attempt to answer some non-intuitive motor design questions through simulation, fundamental equations, and hopefully some homemade discrete 2D EM (static) FEA.

1) What are the tradeoffs of using a larger magnet which provides more H, but increases the reluctance due to magnetic material's low permeability?

• Model an "infinitely long" 5mm diameter cylinder magnet and show diminishing returns for flux at the front of the magnet.
• Then model a coil with a yoke opposing it and increase the distance of the yoke to show diminishing returns there.
• Then with these two plots it should be possible to find an optimal distance, assuming nothing saturates. Some blogs have suggested that an infinitely long magnet is ideal. There must be flux contributed from both the rotor and stator to produce torque, but what is the right balance between these two? The plot below shows increasing magnet thickness (x-axis) and diminishing returns in shear force.

This plot jumps right to the conclusion and shows shear force with increasing magnet thickness along the x-axis. Starting at about 2 mm, we begin to see very diminishing returns in terms of shear force vs. increasing magnet thickness. To be determined is the tradeoff between the PM's contribution and the relative increase from

2) Is there a penalty to having a large insulator (which creates a high reluctance gap) between your motor steel and winding? Is it optimal to ensure that your winding is wrapped tightly against the inductor?

• H field produced is defined as the product of amps flowing through a winding and number of turns in that winding.
• Having a larger diameter coil increases the resistance of the winding, so perhaps the tradeoff is that we are creating a lot of flux that doesn't get used or gets canceled because there are more windings in the way.
• If you have a small steel core at the center of a large diameter of windings are you being punished?

3) What is the effect of filling an air core winding to the core with windings? Diminishing returns? Higher peak flux at center but lower exterior? Would an optimal coil have the smallest possible wall thickness?

• This would be a good one for FEA generally, but there's difficulty in that the ID increasing must effectively mean fewer coils, so it's necessary to compensate for both.

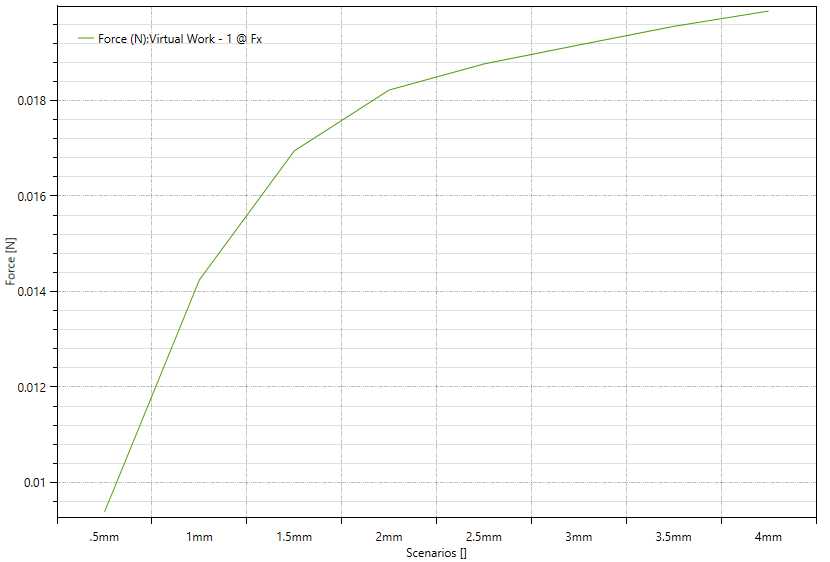
To start a simulation was run with constant amp-turns and increasing ID. Keep in mind that this was run with the optimal displacement as found in the sweep below for a 1mm ID at 2mm displacement. So it's possible that the magnet's location is convoluting this data a bit (more on that later). Interestingly there's a clear inflection point at 3.5mm corresponding to nearly double the shear force created in the .5mm case.

These results provide a strong basis for the possibility that tightly wound inner windings are contributing negatively, and so future sweeps here will need to be run manually to vary ID and have a % reduction in amp-turns corresponding with the coil area lost by increasing the coil's ID.

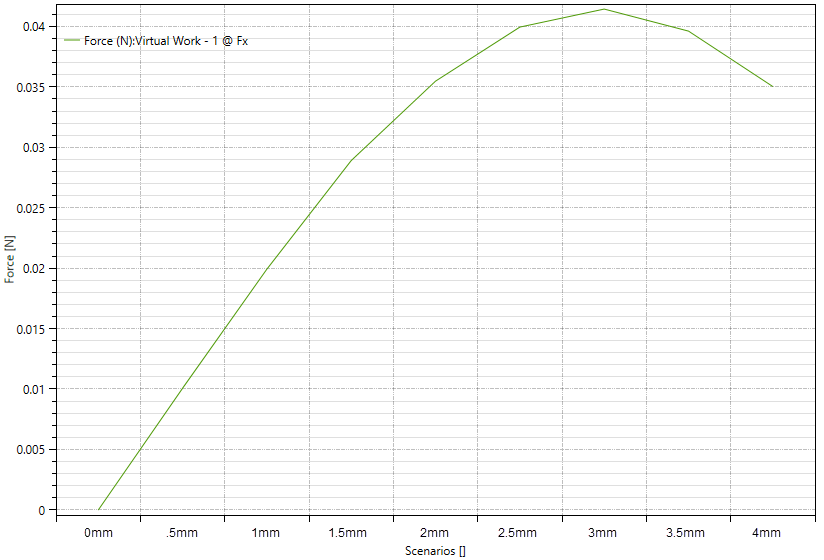
With that said, 3.5mm corresponds with the ID lying almost exactly on the center of the 3mm diameter of the magnet (see image below), so perhaps the takeaway is just that optimal shear will be produced at the point where the ID begins? To test this, lets re-run that offset code to make sure that the "Shear Displacement" parameter is still correctly set to 2mm with a now much larger ID.

Again a sweep for optimal torque producing rotor displacement was run, analogous to load angle (max when 90 deg but unclear for this single pole linear displacement case). See CAD above for exact dimensions. Interestingly with this new ID, the optimal torque producing location has shifted up to 3.5mm. This suggests that iteration after tweaking certain parameters will be necessary to really converge on an optimal solution.

EM Simulations

Towards making a simple 2D simulation tool to answer some of these questions, it seems as though the best place to begin would be to simply model conductors with Biot-Savart:

and (point source) magnetic dipoles with:

Although for the latter it is not clear if a monolithic magnet can indeed be modeled as an array of infinitesimal magnetic dipoles, or if more complex math is required to represent what happens at the corners of a rectangular magnet for example.

Note that it's necessary to model everything with permeability of free space, and if different material permeability are included it will be necessary to converge on a solution with annealing as discussed below.

A note on including materials with changing permeability

The math tells us that B = H x u, which makes it tempting to think that only the magnitude of our B field will change in comparison to H. However the presence of materials of different permeabilities (air vs. steel) will essentially create many small "permanent" magnets which will fundamentally alter

In other words a permanent magnet in infinite free space will have a symmetric B and H field, however if a steel yoke is placed around the right side of the magnet, the B (and H?) field around the left side of the magnet will be significantly reduced.